绘制三次贝塞尔曲线
1. 前言
上一节我们学习了二次贝塞尔曲线,本节我们开始学习三次贝塞尔曲线。贝塞尔曲线都是由一个起点、一个终点和多个控制点组成。二次贝塞尔曲线有一个控制点,三次贝塞尔曲线有两个控制点,n 次贝塞尔曲线就有 n-1 个控制点。
2. 三次贝塞尔曲线
三次贝塞尔曲线是一种三次曲线,它可以向两个方向弯曲,由四个点来定义:两个锚点及两个控制点,控制点用来控制曲线的形状。
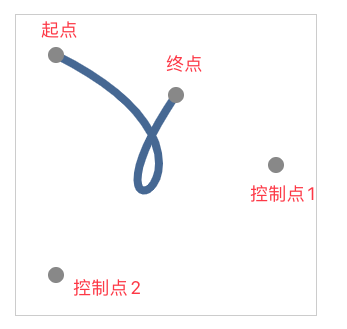
我们先看一下三次贝塞尔曲线的绘制过程:
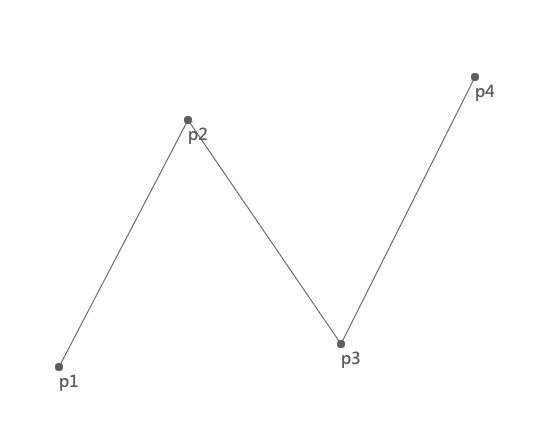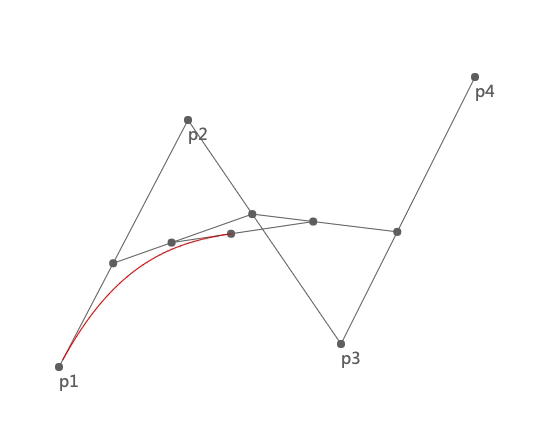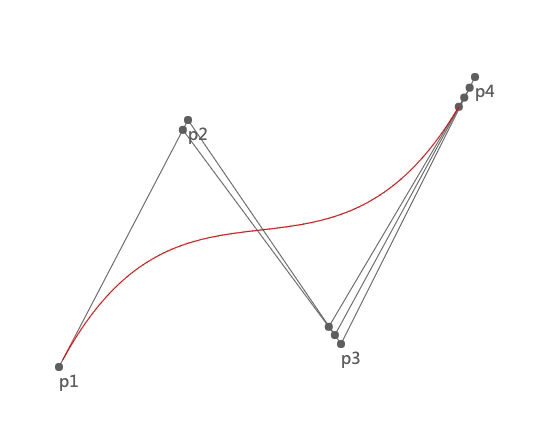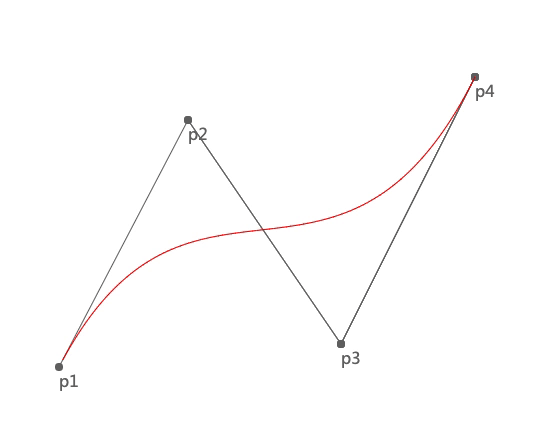
上图中 p1 和 p4 是两个锚点,p2 和 p3 是两个控制点。
在线工具
这里介绍一个开源的在线画贝塞尔曲线的工具,同学们可以体验一下:N阶贝塞尔曲线生成器
canvas 绘制三次贝塞尔曲线
在 canvas 中,绘制三次贝塞尔曲线和绘制二次贝塞尔曲线方法类似,只是比二次贝塞尔曲线多了一个控制点参数,具体绘制方法为:
ctx.bezierCurveTo(cpx1,cpy1,cpx2,cpy2,x,y);
先看整体案例:
运行结果:
这样我们就绘制了一条三次贝塞尔曲线。
3. 方法整理
本小节中我们使用到一个新的方法 bezierCurveTo()。
3.1 bezierCurveTo() 方法
bezierCurveTo 方法作用是绘制一条三次贝塞尔曲线。
变量说明:
| 变量名 | 类型 | 是否必须 | 说明 |
|---|---|---|---|
| cpx1 | Number | 是 | 控制点位置1的X坐标。 |
| cpy1 | Number | 是 | 控制点位置1的Y坐标。 |
| cpx2 | Number | 是 | 控制点位置2的X坐标。 |
| cpy2 | Number | 是 | 控制点位置2的Y坐标。 |
| x | Number | 是 | 终点位置的X坐标。 |
| y | Number | 是 | 终点位置的Y坐标。 |
4. 总结
本小节我们主要学习了利用 bezierCurveTo 方法绘制一条三次贝塞尔曲线,这个方法有6个参数,分别是两个控制点和终点的坐标。
本文来自互联网用户投稿,不拥有所有权,该文观点仅代表作者本人,不代表本站立场。
访问者可将本网站提供的内容或服务用于个人学习、研究或欣赏,以及其他非商业性或非盈利性用途,但同时应遵守著作权法及其他相关法律的规定,不得侵犯本网站及相关权利人的合法权利。
本网站内容原作者如不愿意在本网站刊登内容,请及时通知本站,邮箱:80764001@qq.com,予以删除。
访问者可将本网站提供的内容或服务用于个人学习、研究或欣赏,以及其他非商业性或非盈利性用途,但同时应遵守著作权法及其他相关法律的规定,不得侵犯本网站及相关权利人的合法权利。
本网站内容原作者如不愿意在本网站刊登内容,请及时通知本站,邮箱:80764001@qq.com,予以删除。

